
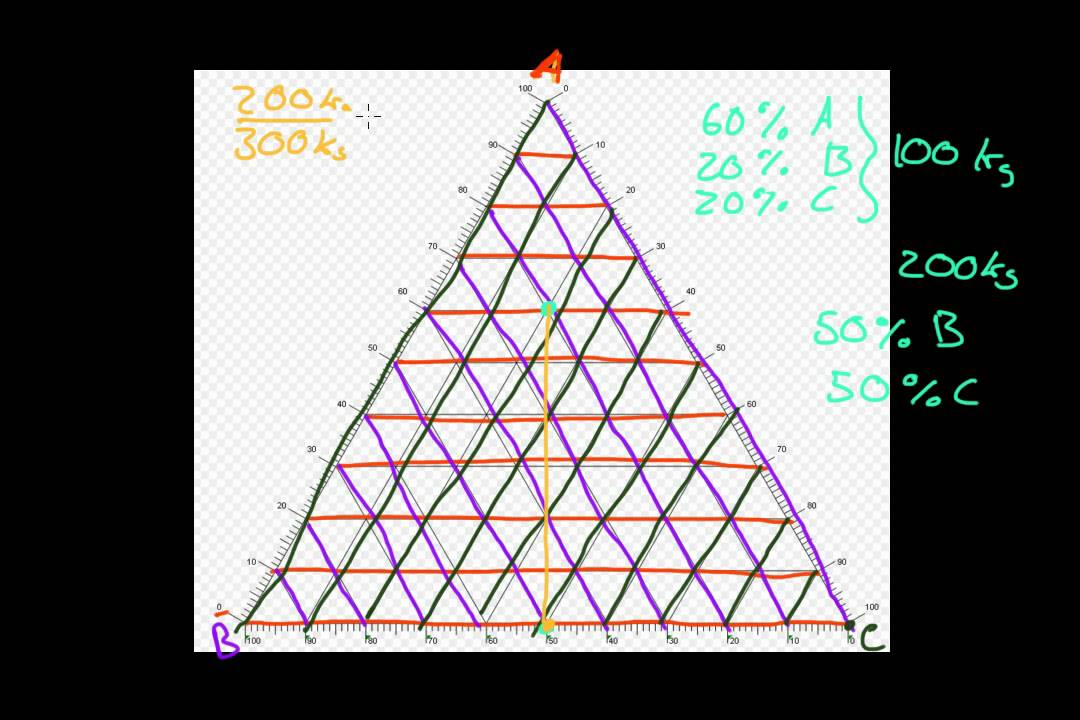
I also tested the ternary diagram, as constructed here, extensively, and the data points plot exactly where they should be (see for instance the first three diagrams (Fig. As per Step 2, the triangle/ternary diagram has then been stretched, so it looks like an equilateral triangle again, which doesn’t affect the XY coordinate system behind it, as it is stretched with it.Ĭorrespondingly, due to the projection of A to Y (100 units), a factor of 0.86603 comes into play: tan(30°) = 0.57735 -> 0.57735 x 0.86603 = 0.5.
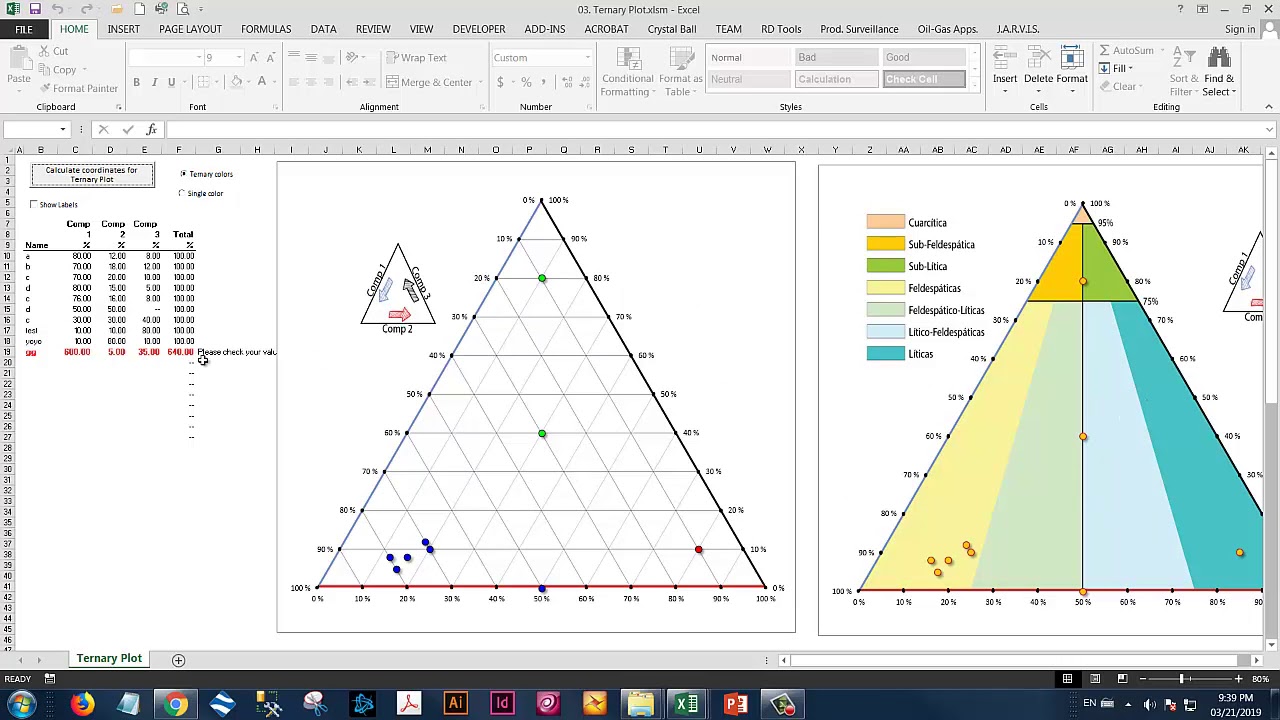
7).īecause A is projected to 100 units (rather than 86.60…), the triangle is elongated and the angle of 30 degrees changes to 26.56505 degrees unfortunately, Excel doesn’t plot diagrams in scale to show this. Thus, we can use the normalized A component as Y without a trigonometric function (Fig. The ternary diagram ABC is projected into a cartesian XY graph.įor an equilateral triangle with a side length of 100 units (e.g., X-axis B-C side 0-100%), the height is 86.60254 units (i.e., Y-axis A).Ī is projected onto Y with 100 units. In the case here, however, it is a different approach: You are right with the tan(30°) statement for calculating the X coordinate in an equilateral triangle/ternary diagram.


 0 kommentar(er)
0 kommentar(er)
